The energy landscape theory of protein folding is a statistical description of a protein's potential surface. It suggests that the most realistic model of a protein is a minimally frustrated heteropolymer with a rugged funnel-like landscape biased toward the native state [1]. This statistical description has been developed using tools from the statistical mechanics of disordered systems, polymers, and phase transitions of finite systems.
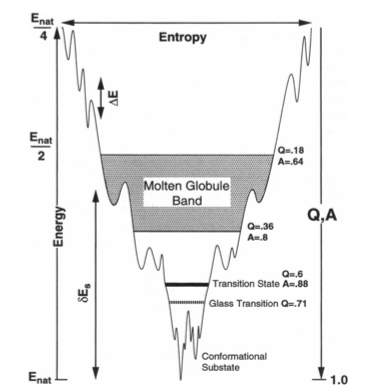
Natural proteins as we observe them today are highly evolved complex systems. Self-assembly and mutual recognition of these polypeptides into defined structural ensembles is a fundamental aspect of the biology of macromolecules, the specificity of which is physically captured by the "Principle of minimal frustration" [2]. This principle states that the energy of the protein decreases more than what may be expected by chance as the protein assumes conformations progressively more like the ground (native) state. In other words, there is a strong energetic bias towards the native basin that overcomes both the asperities of the landscape and ultimately the entropy of the chain. When energetic frustration is low enough, the native energy and folding entropy primarily compete. Since these mainly depend on protein topology, topology becomes a key factor governing folding reactions. It has been shown that the structures of transition state ensembles [3,4], the folding rate [5], the existence of folding intermediates [6], dimerization mechanisms [7], and domain swapping events [8] are often well predicted in models where energetic frustration has been removed and topological information of the native state is the sole input. Still, inhomogeneity in the native contacts energetics, non-native interactions and the residual local frustration present in the native ensemble do contribute to the functional characteristics of proteins, 'molding' the roughness that underlies the detailed protein dynamics [9,10].